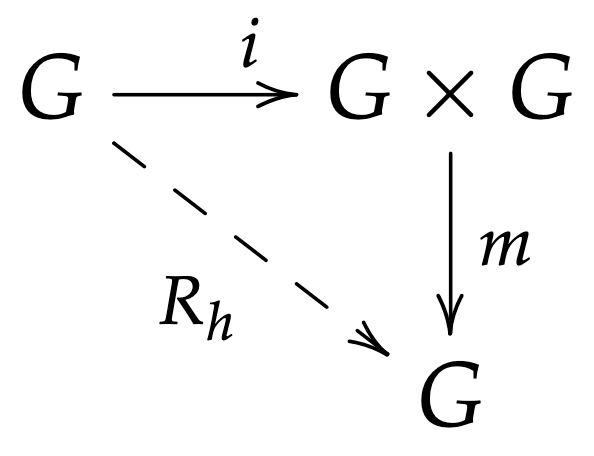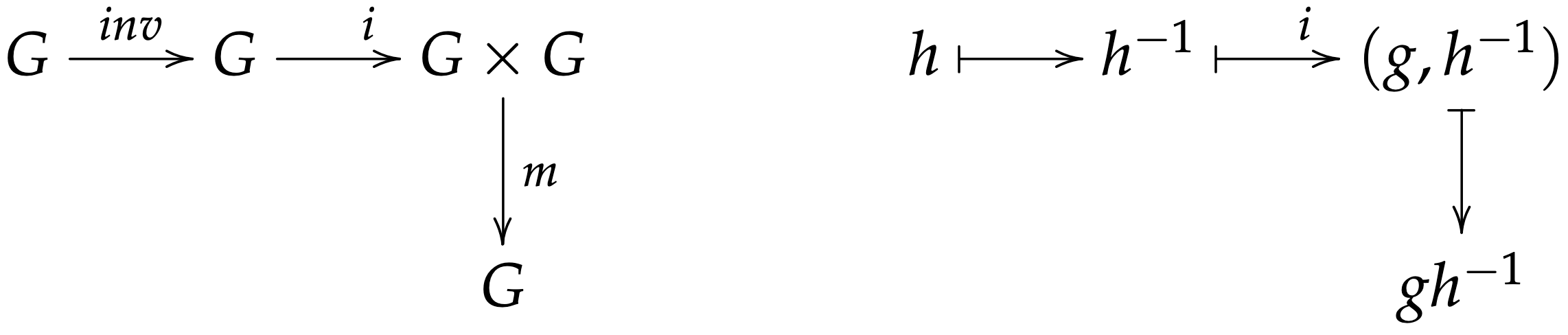3.1 Grupos topológicos

Recordemos que el concepto de espacio topólogico se construyó a partir de un conjunto definiendo una colección de abiertos (o de cerrados). Cuando el conjunto está enriquecido con una estructura de grupo surge un área de la matemática de gran interés llamada Álgebra topológica.

Decimos que un conjunto $G$, equipado con una estructura de grupo y una de espacio topológico, es llamado un grupo topológico si las operaciones mutiplicación> y tomar inversos $$ \begin{cases} m:G\times G\lra G,\;\;(g,h)\mapsto m(g,h):=gh\\ inv:G\lra G,\;\;g\mapsto inv(g):=g^{-1} \end{cases} $$ son funciones continuas. Equivalentemente, $G$ es grupo topológico si y sólo si $(g,h)\mapsto gh^{-1}$ es función continua.

Ejemplos

• Cualquier grupo tiene estructura de grupo topológico al dotarlo de la topología discreta; el resultado es llamado grupo topológico discreto.
• Los espacios producto $\br^n,\bc^n$ son también grupos aditivos con las operaciones usuales de suma y de tomar inverso: $$ m(\ol{x},\ol{y}):=\ol{x}+\ol{y},\qquad inv(\ol{x}):=-\ol{x} $$ Estas operaciones son funciones continuas con la topología euclidiana, por lo que $\br^n,\bc^n$ son grupos topológicos.
• Recordemos que la circunferencia unitaria $S^1$ es subespacio de $\bc$ dado por los complejos unitarios; es además un grupo topológico bajo la multiplicación de números complejos, debido a la propiedad $||z_1z_2||=||z_1||\:||z_2||.$ $\bt$

Para $h\in G$ definimos la multiplicación derecha como la composición de la inclusión con la multiplicación de $G$:

donde $i(g)=(g,h)$ es la inclusión. Observemos que $R_h$ es función continua y tiene por inversa a $R_{h^{-1}}$; es decir, $R_{h}$ es un homeomorfismo. De manera análoga definimos la multiplicación izquierda $L_h(g)=hg$ que tiene por inversa a $L_{h^{-1}}$ y es también homeomorfismo. Con esto obtenemos

Podemos decir un poco más: para cualesquiera $g,h\in G$ existe homeomorfismo $\varphi:G\ra G$ dado por $\varphi=R_{g^{-1}h}$; observemos que $$ \varphi(g)=g(g^{-1}h)=h $$ De igual forma también es posible hacer $\varphi=L_{hg^{-1}}$ para obtener $\varphi(g)=(hg^{-1})g=h$. Por lo anterior se dice que todo grupo topológico $G$ es homogéneo, lo que significa que $G$ tiene la misma estructura topológica alrededor de cualquier punto; es decir, su estructura es homogénea.

$\dem$ $\ida$ Se sigue de inmediato pues todo conjunto finito de un espacio Hausdorff es cerrado.
$\vuelta$ Supongamos $\{e\}$ es cerrado y consideremos $\phi:G\times G\ra G$ definida como $\phi(g,h)=gh^{-1}$. Notemos que $\phi$ se obtiene del diagrama:

de donde se observa que $\phi$ es composición de funciones continuas, por lo que también es continua. Por otro lado, notemos que $$ \phi^{-1}(e)=\{(g,g)\barra g\in G\}=\triangle\subseteq G\times G $$ el cual es cerrado, lo cual es cierto $\sss$ $G$ es Hausdorff.$\findem$

Si $G$ es un grupo topológico y $H\subseteq G$ es subgrupo, entonces, al dotar a $H$ de la topología del subespacio, se tiene que $H$ es grupo topológico llamado subgrupo topológico. Con esto el subgrupo de complejos unitarios $S^1$ es subgrupo topológico de $\bc_*$, los complejos no cero.

3.2 Grupos de matrices

El conjunto de matrices cuadradas $M_n(\br)=M_{n,n}(\br)$ se identifica con el espacio euclidiano $\br^{n^2}$ de la manera usual. La función determinante $\det:M_n(\br) \ra \br$ es una función polinomial en las entradas de $A$, por lo tanto es una función continua. Con esto, el subespacio $\det^{-1}(0)$ es cerrado y su complemento $$ GL_n(\br)= \br^{n^2}\baca det^{-1}(0) $$ consiste de las matrices cuadradas invertibles. Por lo mencionado antes hereda la estructura topológica de $\br^{n^2}$ y además forma un grupo bajo la multiplicación matricial, el cual esta dado por polinomios en las entradas de las matrices por lo que es una operación continua. La función de inversión $A\mapsto A^{-1}$ es una función racional en los coeficientes de $A$ (por la regla de Cramer) por lo que es continua; es decir, $GL_n(\br)$ es un grupo topológico llamado el grupo general lineal real. De manera análoga se define el grupo general lineal complejo $GL_n(\bc)$. Observemos que ambos grupos son Hausdorff.

Los grupos topológicos $GL_n(\br), GL_n(\bc)$ tienen subgrupos muy interesantes:

• $GL_n^+(\br)=\{A\in M_n(\br) \barra \det (A)>0 \}$
• El grupo especial lineal $$ SL_n(\br)=\{A\in M_n(\br) \barra \det (A)=1 \} $$ Notemos que $SL_n(\br)=\det^{-1}(1)$, por lo que $SL_n(\br)$ es subespacio cerrado de $GL_n(\br)$.
• El grupo especial lineal $$ SL_n(\bc)=\{A\in M_n(\bc) \barra \det (A)=1 \} $$ Al igual que antes $SL_n(\bc)$ es subespacio cerrado.
• El grupo especial unitario $$ SU_n(\bc)=U_n(\bc)\cap SL_n(\bc) $$

donde $A^T$ es la matriz traspuesta de $A=[a_{ij}]$ dada por $A^T=[a_{ji}]$ y $\ol{A}^T$ es matriz conjugada hermitiana dada por $\ol{A}^T=[\ol{a_{ij}}]^T=[\ol{a_{ji}}]$. A continuación estudiaremos algunos de los grupos mencionados arriba.

Consideremos $p:M_n(\br)\ra \br^n$ función que manda toda matriz a su primer vector columna. Al considerar la descomposición $M_n(\br)\cong \br^n \times M_{n,n-1}(\br)$, en la que separamos la primera columna, la función $p$ es proyección en el primer factor y por el Lema acerca de proyecciones es función continua y abierta; en particular, la restricción $$ GL_n^+(\br)\lra \br^n\baca \{\ol{0}\} $$ es función continua y abierta. Observemos que por definición de multiplicación matricial se tiene que $p(AB)=Ap(B)=L_A(p(B))$, donde $L_A(B)=AB$ es multiplicación por la izquierda por $A$ y define un homeomorfismo de $GL_n^+(\br)$. Finalmente, dado que todo vector no cero determina un conjunto linealmente independiente de vectores, se sigue que $\forall v\in \br^n\baca \{\ol{0}\} , \:p^{-1}(v)\neq \emptyset$.

Afirm. $L_A(p^{-1}(v))=p^{-1}(Av)$.
Para $C\in L_A(p^{-1}(v))$ existe $B\in p^{-1}(v),\:C=AB$; de aquí $$ p(C)=p(AB)=Ap(B)=Av, $$ por lo que $C\in p^{-1}(Av)$. Por otro lado, sea $C\in p^{-1}(Av)$ y tomemos $B\in GL_n(\br)$ tal que $p(B)=v$; de esto se sigue $$ p(C)=Av=Ap(B)=L_A(p(B)) $$ Así, $C\in L_A(p^{-1}(v)).$ $\bt$

Las propiedades mencionadas arriba se usarán para probar el siguiente:

$\dem$ Procedamos por inducción: observemos que $GL_1^+(\br)=(0,\infty)$, el cual es conexo. Supongamos que $GL_{n-1}^+(\br)$ es conexo. Tomemos la proyección $p$ de arriba y notemos que para $(1,\ldots,0)\in \br^n\baca \{0\}$ $$ p^{-1}((1,0,\ldots,0))=\br^{n-1}\times GL_{n-1}^+(\br) $$ el cual es conexo por hipótesis. Para $y\in \br^n\baca \{0\}$ tomamos $A\in GL_{n}^+(\br)$ tal que $p(A)=y$. De la relación $p(AB)=Ap(B)$ se sigue que $$ L_A(p^{-1}(1, \ldots,0))=p^{-1}(y) $$ por lo que las preimagenes $p^{-1}(y)$ son homeomorfas. Finalmente usamos el Lema \ref{conn} para concluir que $GL_n^+(\br)$ es conexo.$\findem$

La demostración anterior aplica también para $GL_n(\bc)$ probando que es conexo.

$\dem$ Dada una matriz $A$, tomamos su primer vector columna y lo multiplicamos por $1/\det(A)$, con lo que obtenemos las funciones $$ GL_n(\bc)\lra SL_n(\bc),\;\;GL_n^+(\br)\lra SL_n(\br) $$ Dado que estas funciones son continuas y sobreyectivas, del Teorema anterior se sigue la primera afirmación. Para la segunda notemos que se tiene una descomposición $$ GL_n(\br)=GL_n^+(\br)\cup GL_n^-(\br), $$ donde el término $GL_n^-(\br)$ es homeomorfo a $GL_n^+(\br)$ mediante la multiplicación de una matriz con determinante negativo.$\findem$

Ejemplo (El grupo de Heisenberg):

• Consideremos el grupo de matrices triangulares superiores unipotentes $$ H=\begin{Bmatrix}\left(\begin{matrix} 1&x&z\\0&1&y\\0&0&1 \end{matrix}\right) \barra x,y,z\in \bz\end{Bmatrix} $$ Claramente tienen $\det =1$ por lo que $H$ es un subgrupo de $SL_3(\br)$, el grupo de Heisenberg. Por otro lado, como $x,y,z$ pueden ser arbitrariamente grandes se tiene que $H$ no está acotado por lo que no puede ser compacto. En general, los grupos $SL_n(\br),SL_n(\bc)$ no son compactos para $n>1$; véase Ejercicio 4.42 en Manetti, 2015. $\bt$

3.2.1 Matrices ortogonales

Una matriz $A\in M_n(\br)$ tal que $A^TA=I_n$ es llamada matriz ortogonal. Dado que la matriz inversa de una matriz ortogonal $A$ es $A^T$ y como $$ (AB)^T(AB)=B^TA^TAB=BI_nB^T=BB^T=I_n $$ se sigue el conjunto de matrices orgonales $O_n(\br)$ es un grupo llamado el grupo ortogonal real.

Hagamos $A=[a_{ij}]$ y notemos que de la relación $A^TA=I_n$ se tienen $n^2$ ecuaciones: $$ \sum_{k=1}^n a_{ki}a_{kj}=\delta_{ij}, $$ donde $\delta_{ij}$ es la delta de Kronecker definido como $$ \delta_{ij}=\begin{cases} 1,&i=j\\0,&i\neq j \end{cases} $$ Las ecuaciones anteriores muestran que $O_n(\br)$ es un subgrupo cerrado de $GL_n(\br)$.

Consideremos $A\in O_k(\br),\;B\in O_{n-k}(\br)$ y el subgrupo de $O_n(\br)$ dado por $$ \left(\begin{array}{cc} A&0_{k,n-k}\\0_{n-k,k}&B\end{array} \right) $$ Con esto se identifica la inclusión $O_k(\br)\times O_{n-k}(\br)\subset O_n(\br)$.

Notemos que para $A\in O_n(\br)$ $$ (\det A)^2=\det A^T \det A=\det(A^T A)=\det I_n=1 $$ por lo que $O_n(\br)=O_n^+(\br)\cup O_n^-(\br)$, donde $$ SO_n(\br)=O_n^+(\br)=\{A\in O_n(\br)\barra \det A=1\} $$ es llamado el grupo ortogonal especial. Similarmente a lo que se hizo antes, $SO_n(\br)$ se puede expresar como subgrupo de $SO_{n+1}(\br)$ mediante la identificación: $$ \left(\begin{array}{cc} A&0\\0&1\end{array} \right)=\left(\begin{array}{cccc} a_{11}&\cdots&a_{1n}&0\\\vdots&\ddots &\vdots&\vdots\\a_{n1}&\cdots&a_{nn}&0\\0&\cdots&0&1\end{array} \right) $$ para $A=[a_{ij}]\in SO_n(\br)$.

La importancia de los grupos ortogonales se debe a su relación con las isometrías: funciones biyectivas $f:\br^n\ra \br^n$ que preservan distancia; es decir, $|f(x)-f(y)|=|x-y|$. Si $f(0)=0$ entonces se llama una isometrías lineal y en la base canónica corresponde a una matriz en $GL_n(\br)$. Más aún:

Por este resultado (Baker 2001) los elementos de $SO_n(\br)$ son llamados isometrías directas o rotaciones, las cuales están caracterizados por la rotación en $\br^n$ de un plano en un ángulo $\Theta$ respecto a una linea $l$ perpendicular a dicho plano. Más aún, del resultado se sigue que los vectores columnas de una matriz en $SO_n(\br)$ son ortonormales entre si.

Ejemplos:

• Notemos que $SO_1(\br)=\{1\}$, el grupo trivial.
• Tomemos $A\in SO_2(\br)$ y tomemos su primer vector columna, digamos $z\in S^1$. Notemos que el segundo vector columna queda determinado automaticamente: es $iz$, con $i^2=-1$. Más aún, se tiene una biyección $S^1 \leftrightarrow SO_2(\br)$ que, de hecho, es un isomorfismo de grupos (multiplicativos) (Lima 2003).
• Otra forma de ver el isomorfismo anterior es como sigue: consideremos $\mcal{C}\subseteq M_2(\br)$ dado por $$ \mcal{C}=\left\{\left(\begin{array}{cc}a&-b\\b&a\end{array} \right)\barra a,b\in \br \right \} $$ La función $F:\bc\ra \mcal{C}$ dada por $F(a+ib)= \left(\begin{array}{cc}a&-b\\b&a\end{array} \right)$ define un isomorfismo de grupos aditivos. Por restricción a los complejos unitarios $F$ induce un isomorfismo entre $SO_2(\br)$ y $S^1$.
• De las descripciones anteriores podemos describir a $A\in SO_2(\br)$ como sigue: tomemos $z\in S^1$ y lo escribimos $z=\cos(2\pi \alpha)+i\:\sin(2\pi \alpha)$, para algún $\alpha\in [0,1)$. La matriz de rotación tiene la forma $$ \left(\begin{array}{cc}\cos(2\pi \alpha)&-\sin(2\pi \alpha)\\\sin(2\pi \alpha)&\cos(2\pi \alpha)\end{array} \right) $$ y su efecto en un vector $\ol{x}\in \br^2$ está dado por la multiplicación $A\cdot\ol{x}$.
• El grupo de rotaciones $SO_3(\br)$ en $\br^3$ será interpretado como cierto espacio cociente de la esfera llamado el espacio proyectivo $\rp{3}$. Para dimensiones mayores no se tiene ninguna relación entre $\rp{n}$ y $SO_n(\br).$ $\bt$

A continuación un resultado para estudiar las propiedades topológicas del grupo ortogonal:

$\dem$ Consideraremos el caso real. Consideremos la función $$ M_n(\br)\lra M_n(\br)\times \br,\;\;A\mapsto (AA^T,\det (A)) $$ y notemos que la preimagen de $(I,1)$ es $SO_n(\br)$, lo que lo hace subconjunto cerrado de $M_n(\br)$. Por otro lado, dado que para $A=[a_{ij}]\in SO_n(\br)$ se tiene $AA^T=I,\det(A)=1$ los coeficientes pertenecen al conjunto $$ \left\{[a_{ij}]\barra \sum_{i,j}a_{ij}^2=n\right\} $$ probando que $SO_n(\br)$ está acotado y por tanto es compacto.
Para probar la conexidad procedemos como sigue: consideremos la función $$ p:SO_n(\br)\lra S^{n-1} $$ que manda una matriz a su primer vector columna. La función $p$ es continua y además cumple (como ya se probó antes) $$ p(AB)=Ap(B),\;\;L_A(p^{-1}(v))=p^{-1}(Av) $$ mostrando que todas las preimagenes son homeomorfas. Aplicaremos el Lema anterior de arriba para obtener la conexidad de $SO_n(\br)$ para lo cual necesitamos conocer la conexidad de las preimagenes. Primero observemos que $SO_1(\br)=\{1\}$, el cual es conexo. Supongamos que $SO_{n-1}(\br)$ es conexo, y notemos que es la preimagen de $(1,0,\ldots, 0)$. Por el Lema anterior se obtiene que $SO_n(\br)$ es conexo.$\findem$